Math for GameDev - Part 3: Trigonometry
- Categories:
- Math
Freya Holmer published some time ago some classes on the basic maths required for gamedev. Having myself not been a great math student in university I think it is important for myself to have notes in an accessible form. Hope it is useful to someone.
Angles
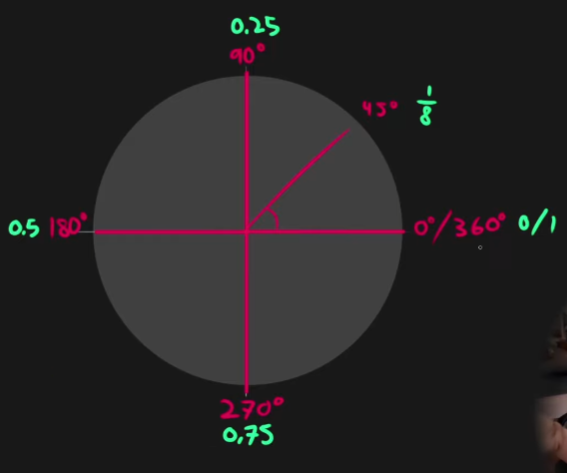
- As vectors, they are relative to a reference point/vector.
- Usually the reference is
Xaxis. - Normally they are represented by greek letters (like most things in maths)
- α ß Γ σ µ δ…
- They can be written using alt+NumPad
- 224, 225, 226, 230, 232, 233, 235
Radians
- 224, 225, 226, 230, 232, 233, 235
Using degrees or decimals to represent a turn is not practical for math usually, most equations and formulas use another system based on RADIANS. Radians term stem from a angle in which the length of an arc, described by two unit vectors, is also 1. It does not really matter, what you really have to know is:
- Unit is based on
1τ = 1tau = 2π- Math people don’t like it generally, but some do and tau fans are very vocal (I don’t really care). Full Turn = 360° = 2π radians = 1τ radians- ` Half Turn = 180° = π radians = 1/2 τ radians`
- …
If you don’t want to use radians, you prefer degrees, then you have to transform by using X° * π/180 = Y radians.
Sine, Cosine, Tangent
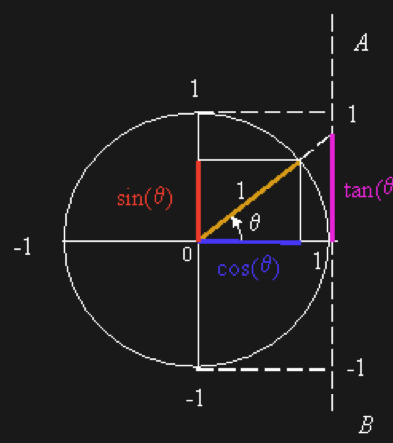
These are definitions the relationship between sides of an arc. Remember back from dot product that projects a vector over another. If those vectors are normalized, the result can be used as the cosine of the angle between those vectors, we have already been using it!
If we transpose one of the vectors in the dot product what we get is the sine of the angle between them!
The tangent is a bit more tricky. Imagine a circle that has radius = 1 as per the unit vectors to determine the angle. To get the tangent we elongate v2 until it crosses a line = l1 that is perpendicular to v1 and starts at the tip of v1. The distance at where it crosses is the value of the tangent.
Triangles
The concepts of sin/cos/tan can also be explained through triangle side relationships. They represent ratios between the length of their sides from which the triangle is viewed:
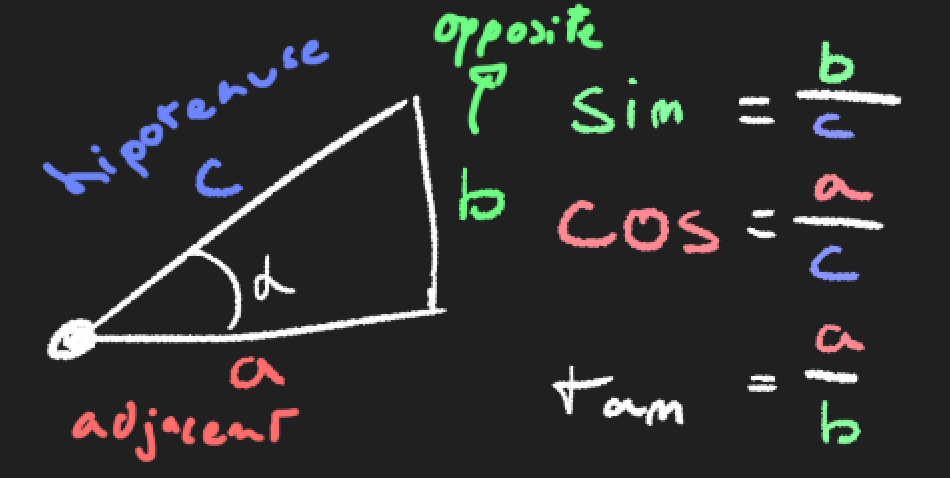
cosine(α) = adjacent / hipotenusesine(α) = opposite / hipotenusetangent(α) = adjacent / opposite
Dot Product
The result of the dot product, the projection of a vector over another, is already a valid result for the cosine between them as long as they are normalized!
Given normalized vectors v and u, ut is the transposed of u(x,y) -> ut(y,x)):
dot(v, u) = cos(angle_v_u)dot(v, ut) = sin(angle_v_u)tan(angle_v_u) = sin/cos- I am lazy, if you want to understand
tanproperly, research. I just need to know that it is a value that can be helpful in getting scalar values from rotations (tangential speed, exit speed, rotation speed…).
- I am lazy, if you want to understand
Angle <-> Vector
Angle represent a rotation with a reference, tehy can’t represent anything if they are not view from a point of reference. Knowing the angle and a reference vector, we can transform from an angle to a new vector.
Given an angle we can obtain 2D Unit Vector:
v.x = cos(α),v.y = sin(α)
Given a 2D Vector and assuming we are using X(1,0) as reference vector:
α = atan(y/x) = atan2(y, x)α = acos(v.x),α = asin(v.y)aSin / aCosare not quite as useful because they can be ambiguous in what orientation the vector represents in the end.
Angle between vectors
Given any 2 normalized vectors v u that are not perfectly parallel:
- α = acos(dot(v, u))
Example 1: Solve the sides of a triangle, given a set of information
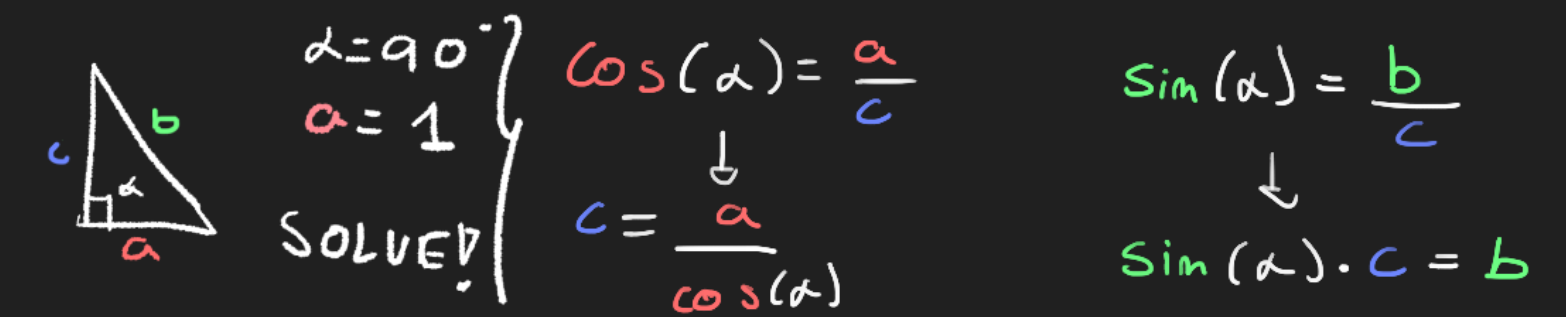
Having solved that, we can find the other angles by performing the inverse operations with the known sides:
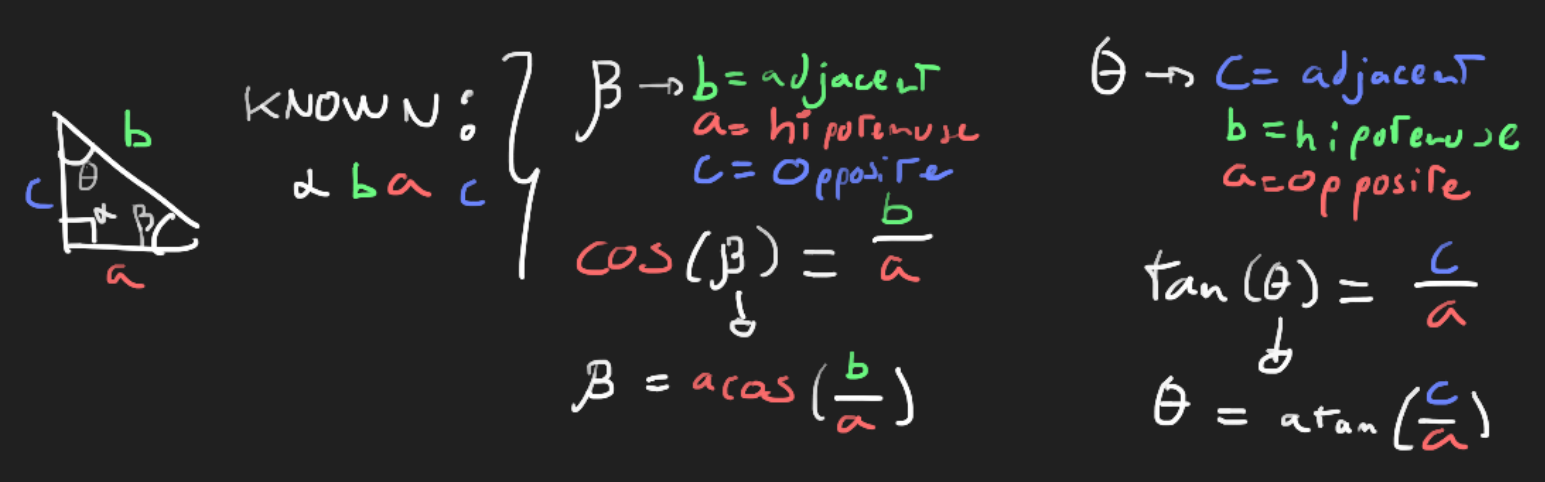
Extra: Determinant
There is a concept with matrices which is its determinant. This value can be calculated from square matrices (aka 2x2,3x3,…, NxN) and is used to obtain the inverse, solving linear equations and more things I do not know about. For knowing more about it go to mathisfun.com or research it.
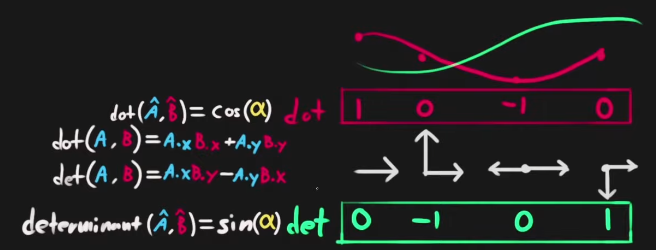
What is important for us is that with 2D Vectors, the determinant of a matrix composed by 2 2D Vectors is basically another “form of dot product” but instead of obtaining the cosine, we get the sine:
dot(a,b) = a.x * b.x + a.y * b.y = cos(angle_a_b);
det(a,b) = a.x * b.y - a.y * b.x = sin(angle_a_b);
Our actual use-case, is instead of wanting to know how much is a vector is looking at a certain direction, it would be how much is it perpendicular to the vector (Right being positive).
Exercise 7: Draw Regular Polygons
Given that all sides in a regular polygon have the same length, the angle in each vertex is also the same; draw any multiple size polygon given a number of sides and side size:
// Given that all sides are regular, we know that all vertices will be at the same length
// To find where the vertices are, we need to know the rotation they are in respect to the first one
// which we will place at angle 0.
// We know how to translate a rotation to vector, so we apply it to obtain unit vectors at intervals
// based on the side
List<Vector2> vertices = new List<Vector2>();
Vector2 center = transform.position;
// The angle will be a full rotation divided by num of sides
float rot_angle = 2.0f*Mathf.PI/sides;
for(int i = 0; i < sides; ++i)
{
// We use the cos to get x, and sin to get y
// Then we scale it and translate it with the center
Vector2 vec = (new Vector2(Mathf.Cos(rot_angle*i), Mathf.Sin(rot_angle*i))) * length + center;
vertices.Add(vec);
}
// Then to draw them we just need to draw from one vertex to another
// I added a skip value to get star type shapes!
// The star shape must go from 1 to num_sides
for(int i = 0; i < sides; ++i)
{
int next = (i + vert_skip > sides-1) ? i+vert_skip - sides : i+vert_skip;
Gizmos.DrawLine(vertices[i], vertices[next]);
}

Exercise 8: Adaptative FOV
A - Based on a bunch of points and a direction, get FOV to fit them all
// As seen previously, the dot product gives us how much a vector is looking at a given direction
// We need just the vector that is the direciton and a normalized vector from camera to points
Camera cam = GetComponent<Camera>();
Vector2 dir = cam.transform.right;
Vector2 pos = cam.transform.position.normalized;
float widest_angle = 1; // The minimum angle is 0 which has cos = 1
for(int i = 0; i < num_points; ++i)
{
Vector2 point = (points[i] - pos).normalized;
float dot_res = Vector2.Dot(dir, point);
widest_angle = (dot_res < widest_angle) ? dot_res : widest_angle;
}
// Known the widest angle, we transform angle to vector
// For the other part, we cahgne Y direction
// (Not accounting for camera rotationa and assuming lookign at perfect right or left)
Gizmos.DrawLine(pos, pos + 100 * (new Vector2(widest_angle, Mathf.Sin(Mathf.Acos(widest_angle)))));
Gizmos.DrawLine(pos, pos + 100 * (new Vector2(widest_angle, Mathf.Sin(-Mathf.Acos(widest_angle)))));
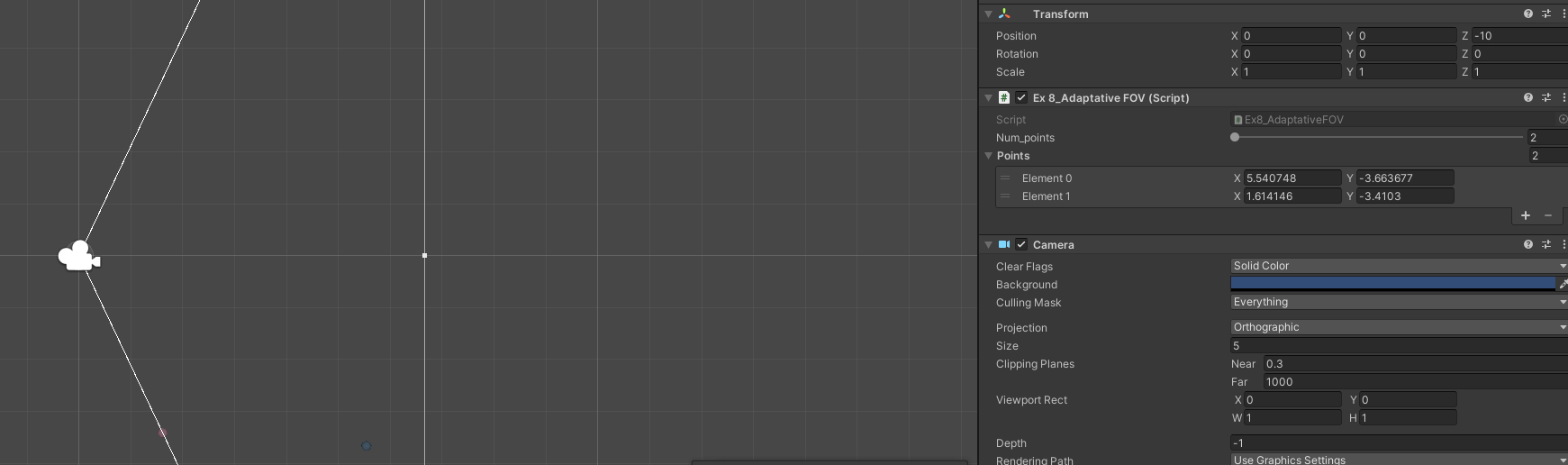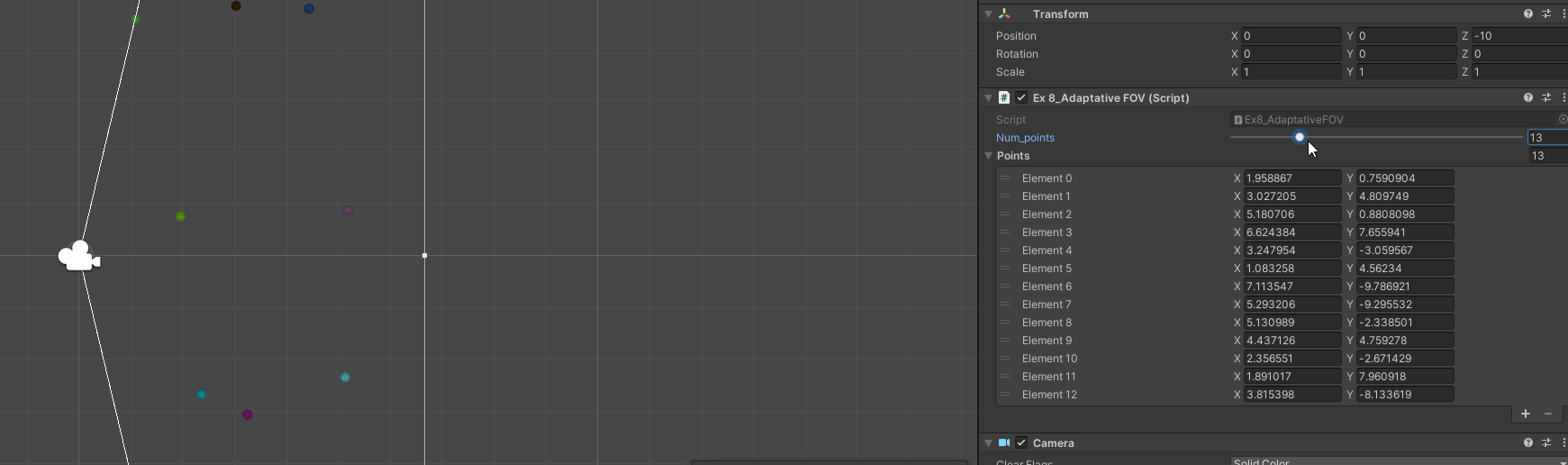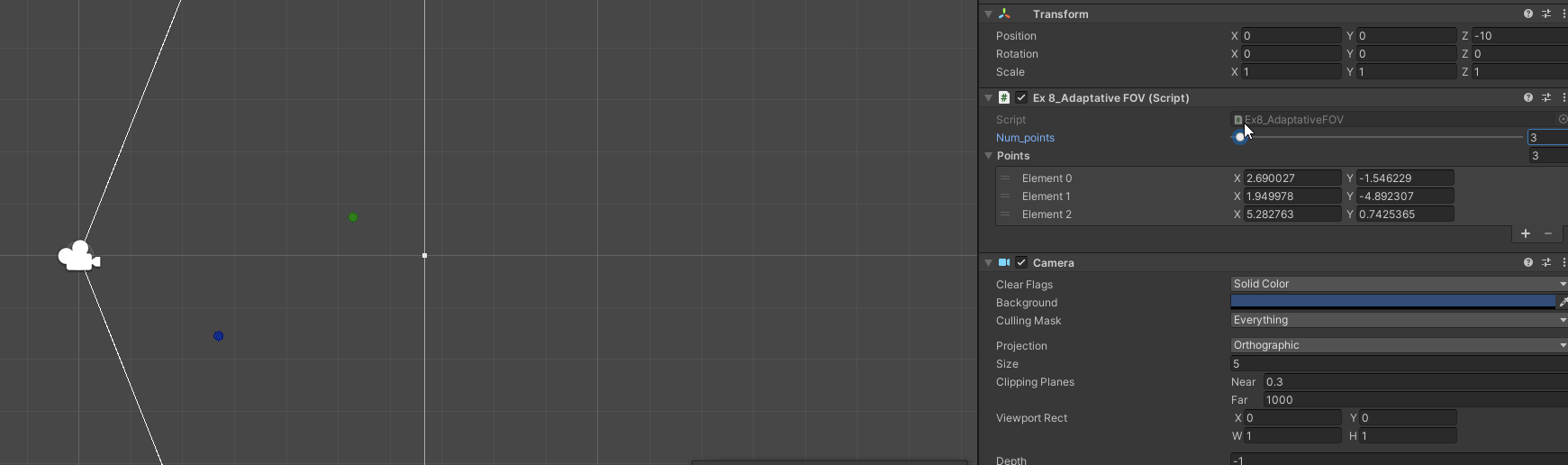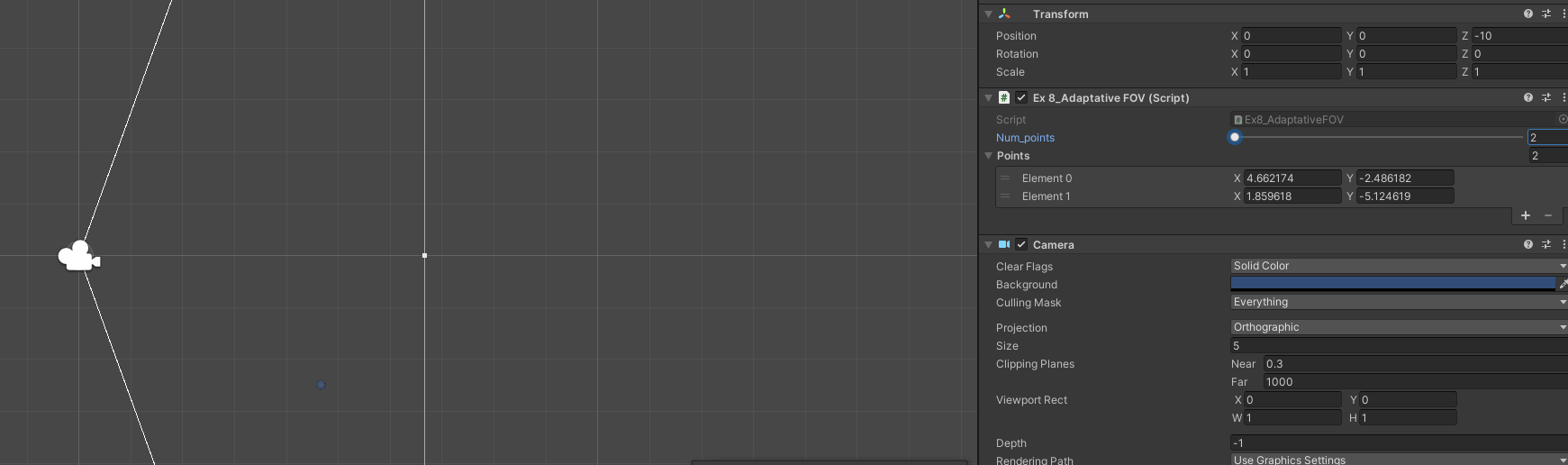
B - Account for bounding box of the points
// To do this, we are calculating an extra angle
// That angle is the one between the point vector and the tangential vector
// The tangential vector is known to have an angle of 90°, a side of size Radius
// and a side of size Length(camera to distance)
// These sides will be the Opposite (radius) and Hipotenuse(point_dist) of the angle we want
// this we get the angle with Sine
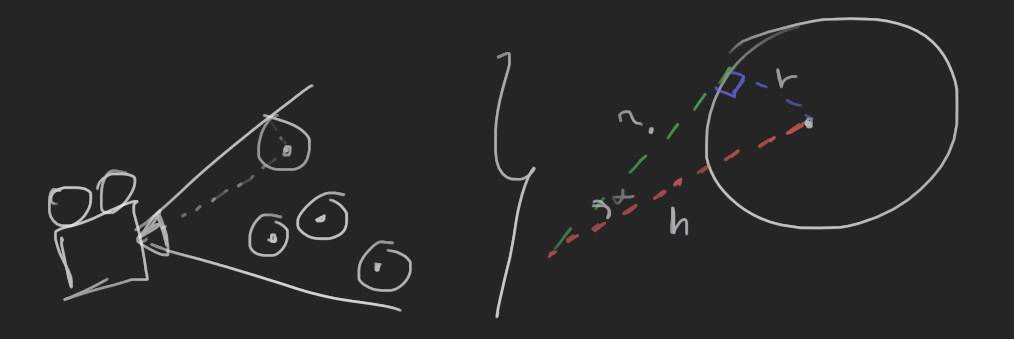
// We change basically the calcs inside the loop for each point
Vector2 point = points[i] - new Vector2(cam.transform.position.x, cam.transform.position.y);
float angle_rad = Mathf.Asin(radius / point.magnitude);
float dot_res = Vector2.Dot(dir, point.normalized);
float cos_min = Mathf.Cos(Mathf.Acos(dot_res) + angle_rad);
float cos_max = Mathf.Cos(Mathf.Acos(dot_res) - angle_rad);
// But we have to test with the min/max angles
widest_angle = (cos_max < widest_angle) ? cos_max : widest_angle;
widest_angle = (cos_min < widest_angle) ? cos_min : widest_angle;
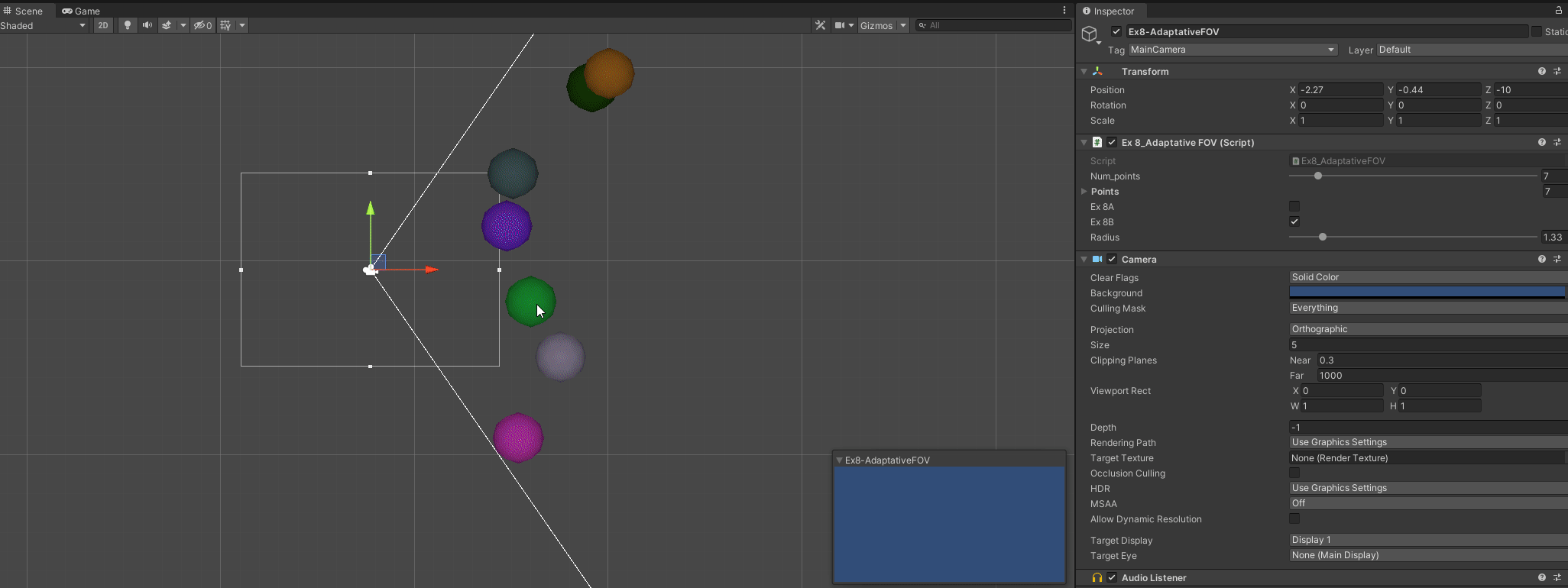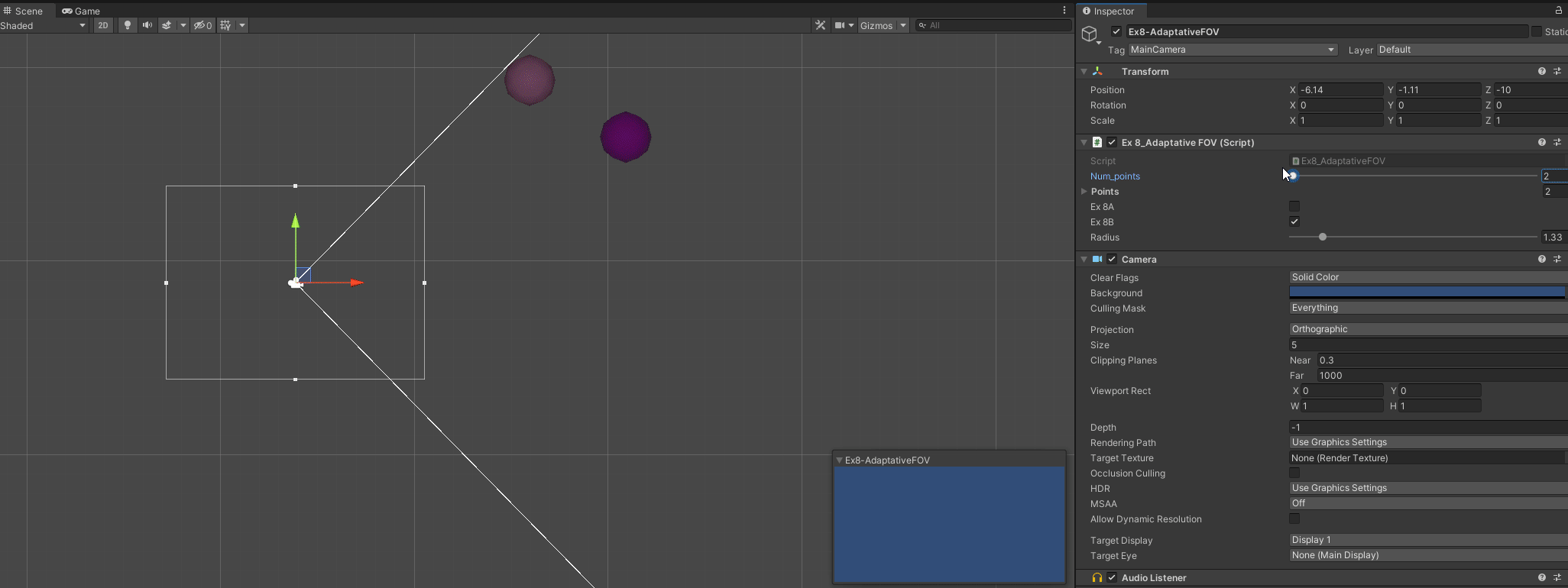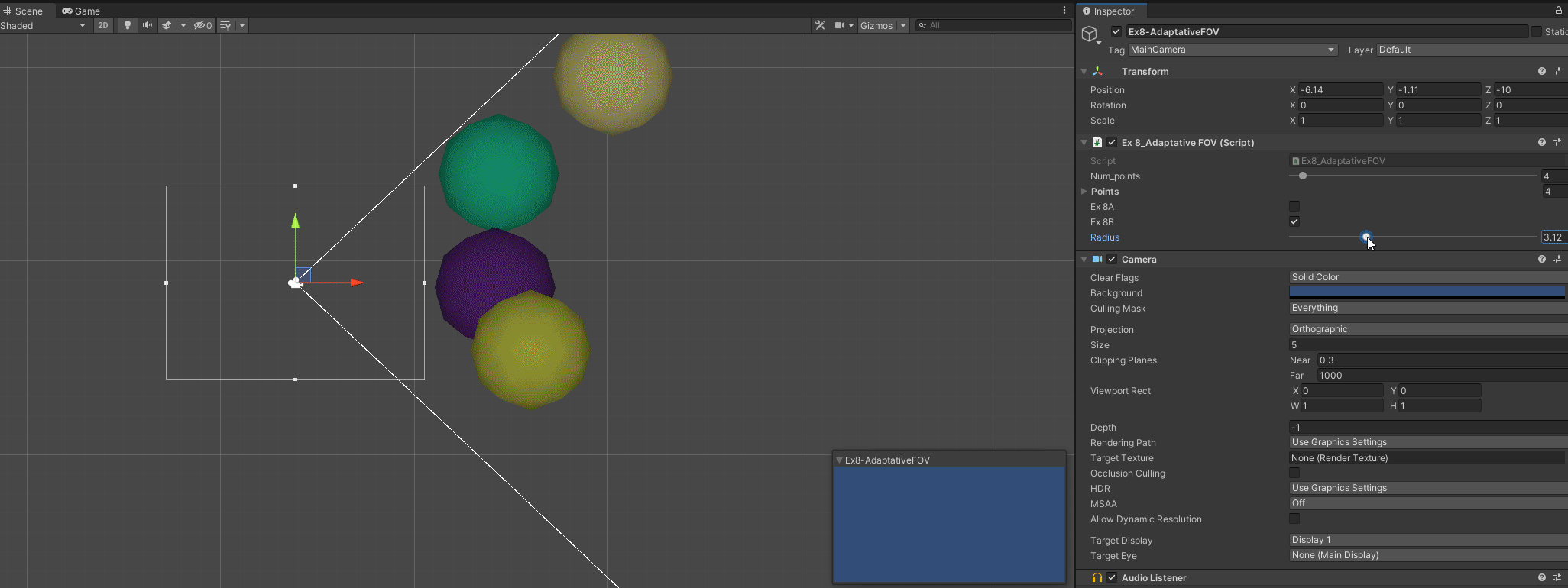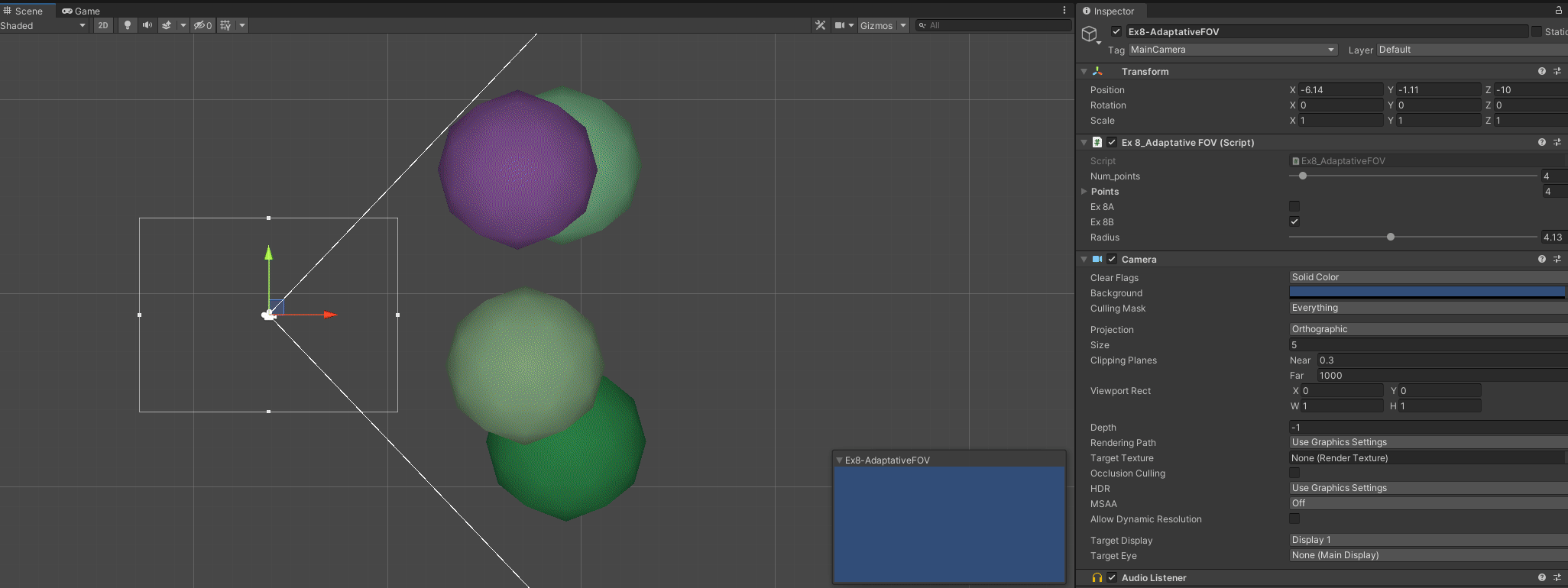
C - Make it work for any direction
On the previous exercices, I used debug lines to represent a field of view instead of using the actual field of view to be representative. That would bring about issues when actually wanting to fit points. At the same time, they were not liable to changes in rotation.
To make sure it works, now we will be generating the points in 3D and making it work with any rotation as long as all points are constrained in the forward direction of the camera.
// Inside the point test loop
// We transform our point to the local space of the camera
Vector3 point_cam_space = cam.transform.InverseTransformPoint(points[i]);
// We want to test using 2D angles, thus we can just assume the following:
// Our new X axis is the currecnt cam.forward, but in local space that will be (0,0,1)
// The transformed points Z position will now be the X position
// As we don't care about the new Z position (old X axis), we can use a Z,Y vector to represent the point in 2D
Vector2 point = new Vector2(point_cam_space.z, point_cam_space.y);
// rest is the same
float angle_rad = Mathf.Asin(radius / point.magnitude);
float dot_res = Vector2.Dot(dir, point.normalized);
float angle_point = Mathf.Acos(dot_res);
float cos_min = Mathf.Cos(angle_point + angle_rad);
float cos_max = Mathf.Cos(angle_point - angle_rad);
widest_angle = (cos_max < widest_angle) ? cos_max : widest_angle;
widest_angle = (cos_min < widest_angle) ? cos_min : widest_angle;
// Then we just transform the widest angle to actual angle
cam.fieldOfView = Mathf.Rad2Deg * Mathf.Acos(widest_angle) * 2;
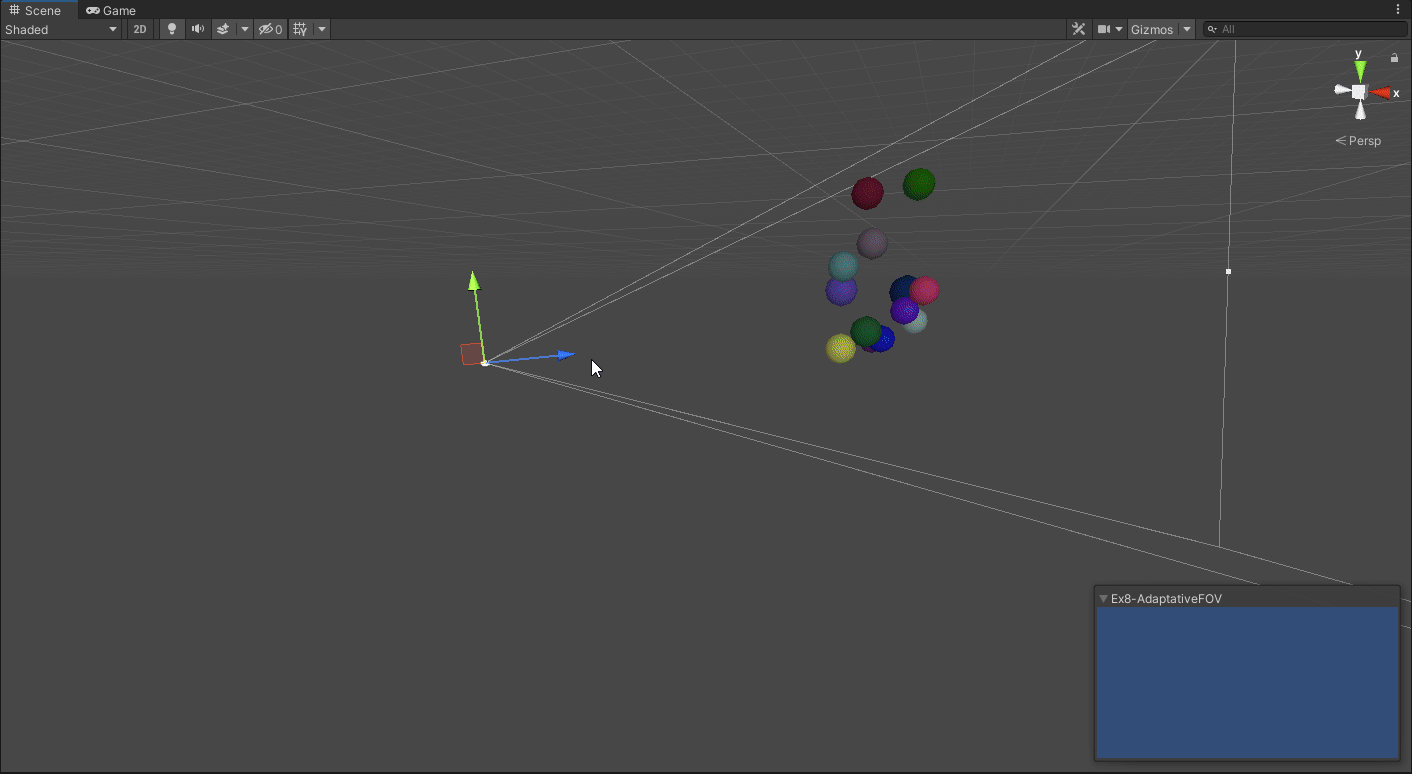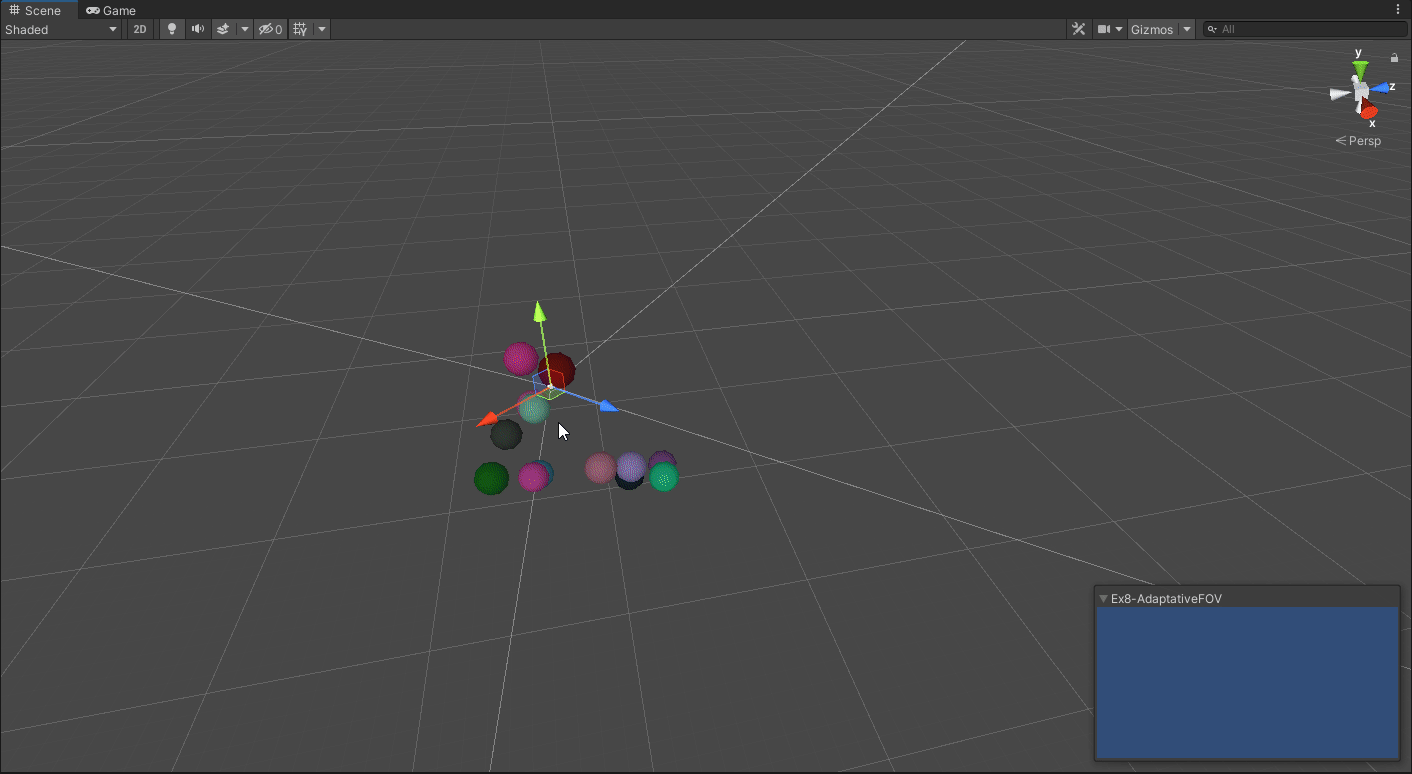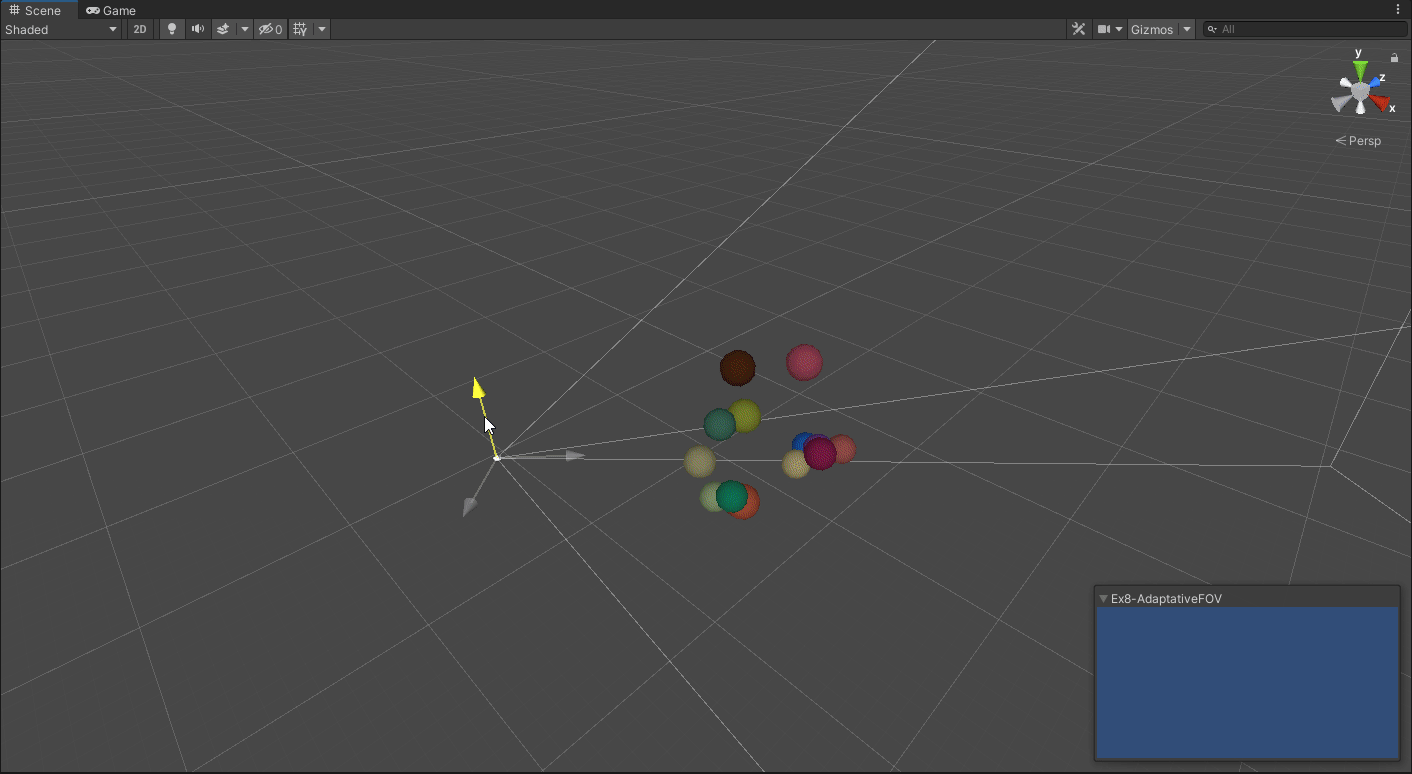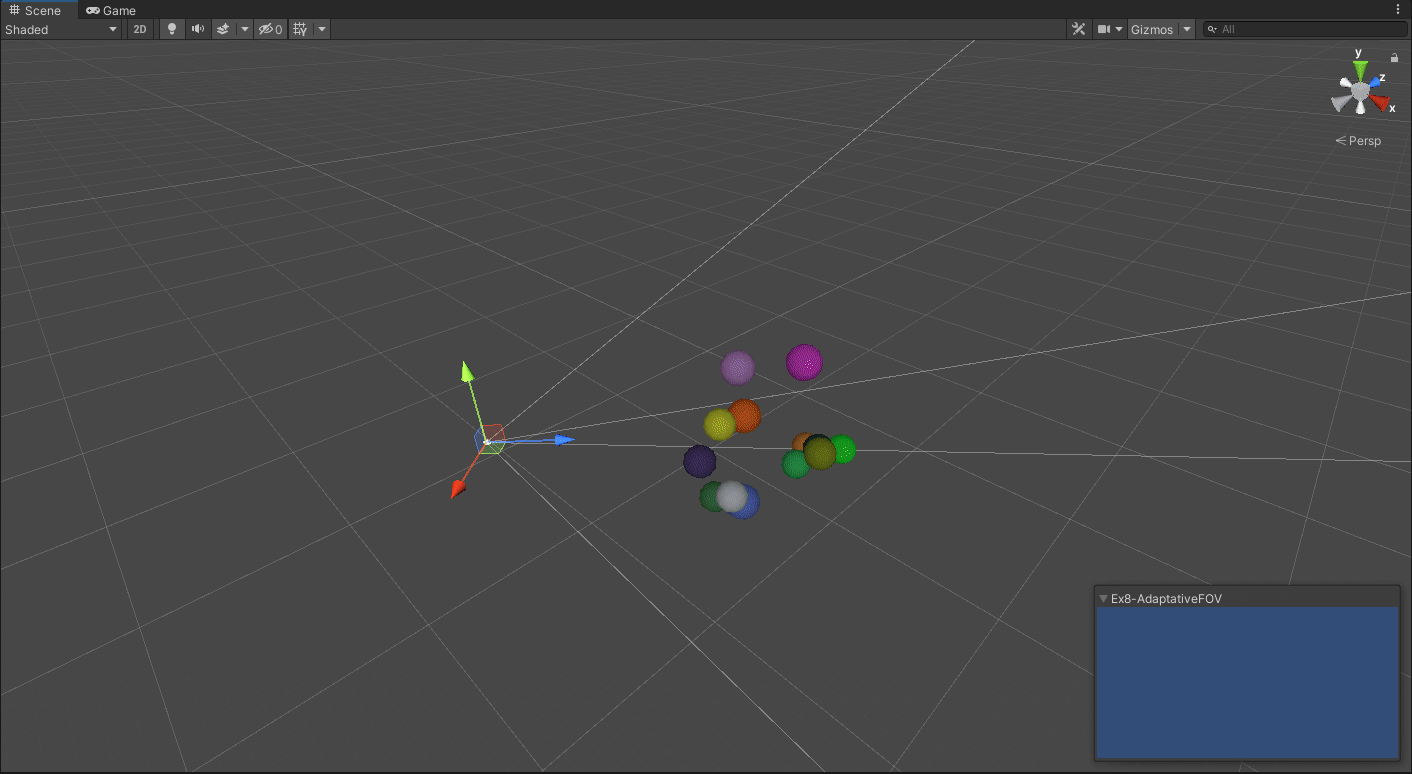
Afterwords
This series of posts are mainly for my own use. Everyone understands concepts in different ways, after a lot of time battling ways of working (which unfortunately during my studies have been based mostly on crunching) I have found out that having accessible notes on things is the best way. I am awful at remembering thigns correctly and have to check things constantly.
For any other person that does think this theme is useful to them, check Freya Holmer’s Youtube Channel, as most of her content is already uploaded there!
A special mention is that in the last exercise I had some issues understanding space transformations and understanding Unity Camera, that’s why i decided on drawing Gizmos on the first exercises to represent it properly, assuming a dir = (1,0).