Math for GameDev - Part 2: Spaces, Matrices & Cross Product

Freya Holmer published some time ago some classes on the basic maths required for gamedev. Having myself not been a great math student in university I think it is important for myself to have notes in an accessible form. Hope it is useful to someone.

SPACES - From Part 1. Ex.3

Most things are relative to others. When we decide that an object has a certain position, that is relative to our WorldSpace defined by our main axis X(1,0,0) , Y(0,1,0) , Z(0,0,1). But that space can also be relative to another object, axis or space that we define.

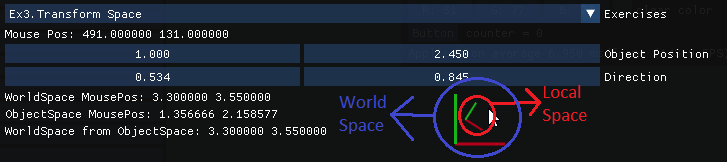
DEFINE IN VARIABLES WHICH SPACE YOU ARE WORKING IN !

Inconsistencies - Engines, Libraries and Tools

There is a concept for defining the world space and rotations called the “The Right Hand Rule”. This concept is bullcrap because everyone uses it in different ways, so there is “The Left Hand Rule” as well as modified positions. Just know that I am used to the previous world space referred (X = Right, Y = Up, Z = Forward) but some engines, libraries and tools do things in other ways and you have to get used to their space.

This will be further explained with the cross product.

Matrices

When we define a world orientation and axis, we are defining the basis vectors which are the ones that define the pillars of the world space, in my case I decidedd X(1,0,0) , Y(0,1,0) , Z(0,0,1).

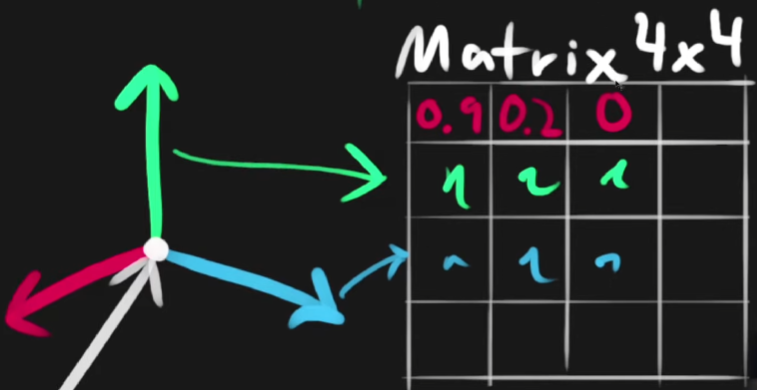
To define an object in said space, we need to define a position relative to that, its rotation in their world and a scale for the object. That composition of data is called a Transform which is stored in a matrix.

When storing such Transform we are saving the basis vectors of the object which are relative to another space.

Data Layout

Understanding first that matrices represent an array of value in n dimentions, such as that we can obtain values as we would in an array (mat4x4 ~= arr[4][4) we can now understand the layout for further operations.

Why Matrices?

Because we can multiply matrices by a vector and obtain another vector. Basically, we are transforming a vector into the space defined by the matrix!

Matrix4x4 mat;
Vector4 v; // (x,y,z,w)

Vector4 result = mat * v;
/*
    mat * v
    {
        result.x = mat[0,0]*v.x + mat[0][1]*v.y + mat[0][2]*v.z + mat[0][3]*v.w;
        result.y = mat[1,0]*v.x + mat[1][1]*v.y + mat[1][2]*v.z + mat[1][3]*v.w;
        result.z = mat[2,0]*v.x + mat[2][1]*v.y + mat[2][2]*v.z + mat[2][3]*v.w;
        result.w = mat[3,0]*v.x + mat[3][1]*v.y + mat[3][2]*v.z + mat[3][3]*v.w; 
    }
*/

The newly added 4th coordinate to the Vector4 serves right now to determine if we want to use the position in order to transform the vector. If w = 0 the last operation will not take the position in the matrix into account (mat[0-2][2]).

When we are transform from Local to World we apply the multiplication directly, but when we do the inverse we apply the inverse matrix to it!

most enignes and libraries will provide a way to invert a matrix or have it cached every time is changed...

A small “Tangent”

Sometimes we just want to represent a rotation, which does not require the full Matrix4x4 and a Vector4. For that we can define a Matrix3x3 which contains such direction vectors:

Cross Product cross(a,b) = A x B = Vector

Another way of multiplying vectors, yey! Given 2 vectors that are not equal, we can calculate a perpendicular one!

The Right/Left Hand rule

In Physics/Math there is the concept of the Left/Right hand rule to determine how some forces interact in different axis. For game you will have to adapt to whatever rule the creator decided on, as each component can very well be flipped in either their positive or negative poles or even flipping hand and axis naming.

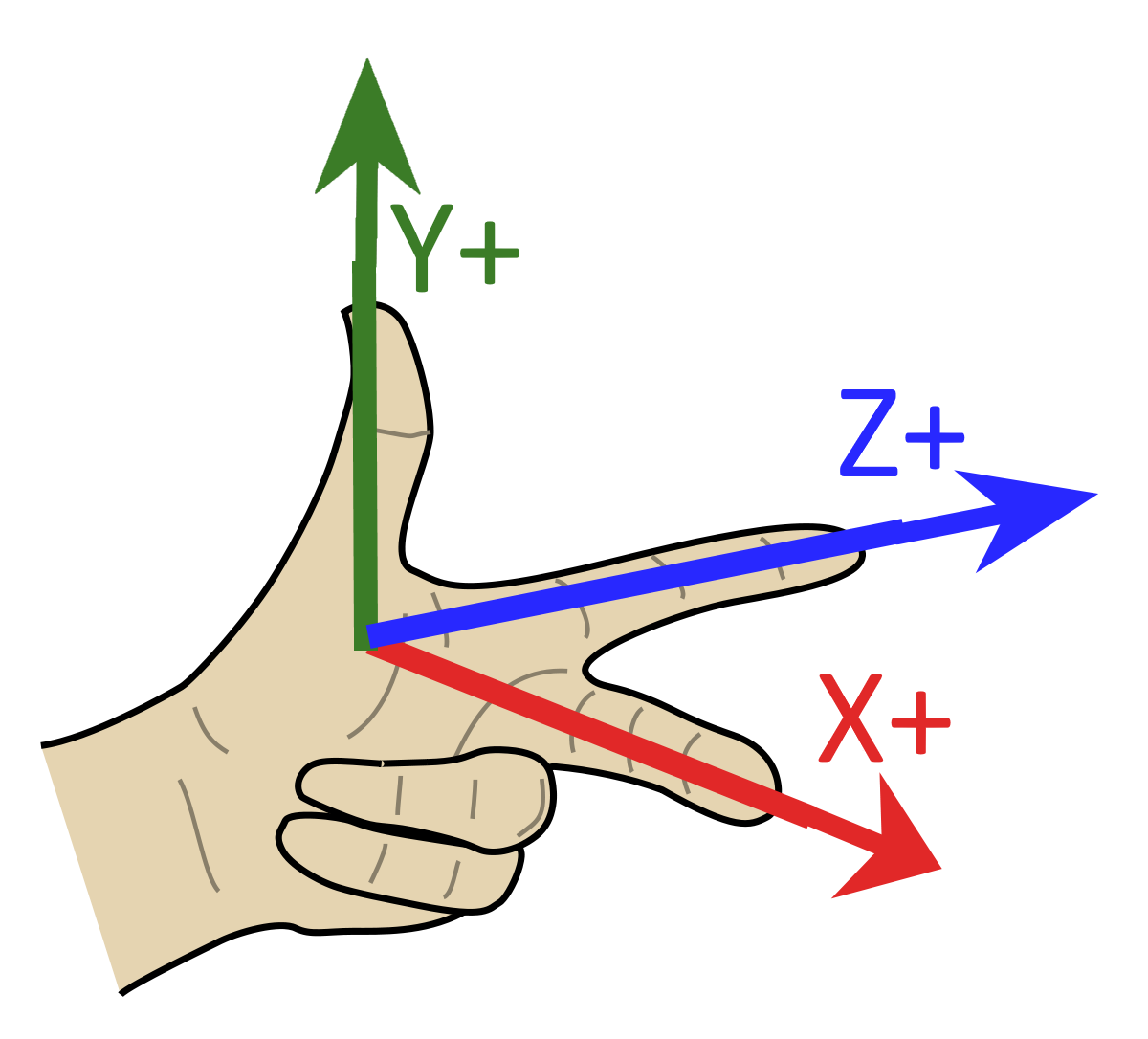
If we input the vectors in the order that the rule is set int he tool, the result of the Cross Product will be perpendicular positive to the other two.

Calculating the Cross Product

Vector3 cross(Vector3 a, Vector3 b)
{
    Vector3 ret;
    ret.x = a.y*b.z - a.z*b.y;
    ret.y = a.z*b.x - a.x*b.z;
    ret.z = a.x*b.y - a.y*b.x;
    return ret;
}

// Second Definition of Cross Product = |a x b| = |a| * |b| * sin(angle_ab)
float AngleBetween(Vector3 a, Vector3 b)
{
    Vector3 cross = cross(a,b);
    float sin_angle_ab = length(cross) / (length(a) * length(b));
    return arc_sin(sin_angle_ab);
}

Exercise 4 - Reflecting Ray

Given a point and a direction, get the ray that would reflect from hitting a surface.

// Assuming we have a function to cast rays and get returned a raycast hit
// A raycast hit would return a position and the orientation of the geometry at the hit point (Normal!)

// Dot gives you de project of direction over normal
// So we can create a vector that is the normal, adjusted to the vector sent!
// If we were to subtract this adjusted_normal to direction, we would get a vector that
// goes forward perpendicular to the normal, as it is adjusted to the projection
// If instead we subtract the adjusted_normal but double in size, it will mirror the vector!

Vector3 position, direction;
RaycastHit hit = RayCast(position, direction);
Vector3 adjusted_normal = 2*dot(direction, hit.normal)*hit.normal;
Vector3 mirror_normal = 2*adjusted_normal;
Vector3 reflected = normalize(direction - mirror_normal);

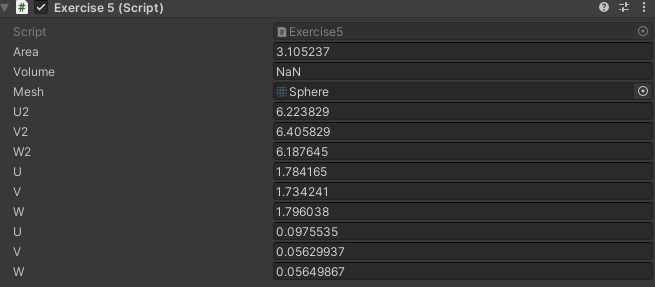
Exercise 5 - Surface area of a mesh

Given a mesh that is made of triangle primitives area = (w * h)/2 = (length(v2 - v1) * length(v3 - v1))/2, calculate its area and volume.


// The volume calculations are incorrect, I can't properly understand it
// Tried following this: http://zobayer.blogspot.com/2009/11/volume-of-irregular-tetrahedron.html

Vector3 mesh_center; // assume the mesh has a center that all points are around it
// Else it should be required to have multiple centers and areas to divide the calculations...
float area = 0, volume = 0;

Vector3 verts[];
int indices[];

for(int i = 0; i < indices.size(); i+=3)
{
    // Area
    Vector3 a = verts[indices[i]];
    Vector3 b = verts[indices[i+1]];
    Vector3 c = verts[indices[i+2]];
    area += length(cross(b-a, c-a) /2.f;

    // Volume
    float U = length(b-a);
    float V = length(c-b);
    float W = length(a-c);
    float u = length(transform.position - c);
    float v = length(transform.position - a);
    float w = length(transform.position - b);
    volume += TriMeshVolume(u, v, w, U, V, W);
}

// Volume Functions - Not translated to pseudocode from Unity

private float TriVolumePair(float a, float b, float c)
{
    return Mathf.Pow(a,2) + Mathf.Pow(b,2) - Mathf.Pow(c,2);
}

private float TriVolumCalc(float u, float v, float w, float u2, float v2, float w2)
{
    return Mathf.Sqrt(4*Mathf.Pow(u,2)*Mathf.Pow(v,2)*Mathf.Pow(w,2) - Mathf.Pow(u,2)*Mathf.Pow(u2, 2) - Mathf.Pow(v,2)*Mathf.Pow(v2, 2) - Mathf.Pow(w,2)*Mathf.Pow(w2, 2) + u2*v2*w2) / 12;
}

public float u2, v2, w2;
private float TriMeshVolume(float u, float v, float w, float U, float V, float W) {
    u2 = TriVolumePair(v, w, U);
    v2 = TriVolumePair(w, u, V);
    w2 = TriVolumePair(u, v, W);
    return TriVolumCalc(u,v,w, u2, v2, w2);
}

Exercise 6 - Turret Placement - Normal,Tangent,Bitangent

When we want to place something in our world, we need to know where that object will be facing. Given a position and a direction, obtain the direction which the object should be placed on top of a terrain, which is the Normal vector, the direction it is looking (Tangent) and the Bitangent.

Vector3 position, direction;

RaycastHit hit = RayCast(position, direction);
Vector3 tangent = normalize(cross(direction, hit.normal));
Vector3 bitangent = normalize(cross(direction, tangent));

Afterwords

This series of posts are mainly for my own use. Everyone understands concepts in different ways, after a lot of time battling ways of working (which unfortunately during my studies have been based mostly on crunching) I have found out that having accessible notes on things is the best way. I am awful at remembering thigns correctly and have to check things constantly.

For any other person that does think this theme is useful to them, check Freya Holmer’s Youtube Channel, as most of her content is already uploaded there!

LinkedIn Reddit