Math for GameDev - Part 1: Vectors & Dot product
- Categories:
- Math
Freya Holmer published some time ago some classes on the basic maths required for gamedev. Having myself not been a great math student in university I think it is important for myself to have notes in an accessible form. Hope it is useful to someone.
Vectors Basics - 1D
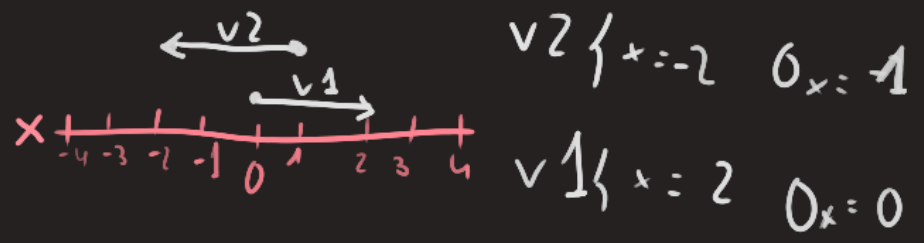
Vectors by themselves just represent a point relative to an other origin point. In the base example, v2 has the origin in 1 but ends in -2, the vector itself is v2(-3). v1 on the other hand starts at our arbitrary origin thus the component x being the representative of the vector itself v1(2).
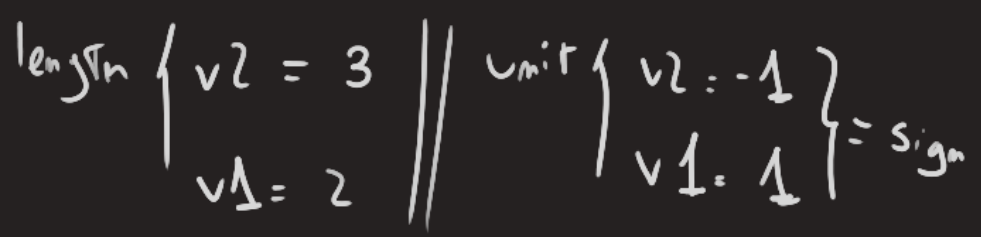
length: absolute magnitude or scalar size of a vector. Calculating the magnitude of a vector varies by dimentions, explained later.absolute: refering to the positive part of numbers, also known as unsigned.direction: unit representation of a vectorunit / normalized vector: vector which its length is 1. Basicallyv / length(v) = (vx / length(v), vy / length(v), ...)h(v), …)`sign(v): general representation of the direction of a vector. It should return a vector according to the vector dimention input, normalized (length = 1).- A
0 directionvector, can be interpreted in a variety of way. Generally we want 1 to be returned in programming but your mileage may vary.
- A
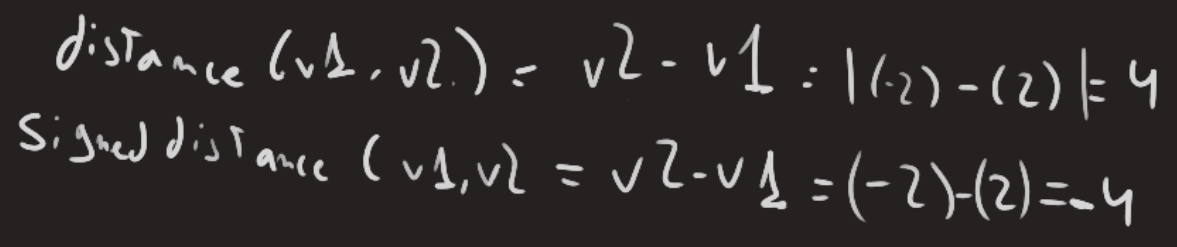
distance: length of the vector that joins two positions :abs(length(vB - vA))signed distance: usually we use the positive term of a distance, sometimes we want also a negative want, thuse we don’t get the absolute : `length(vB - vA)
When using more dimentions you will want to use different colors per dimention. Usually, we use RGB color space to map to XYZ axis.
Adding new dimentions in an orthographic space, each new axis will be perpendicular ot the previous ones.
Vectors really define a point in space from a defined 0o (Origin point).
2D Vectors - vector2D(x, y)
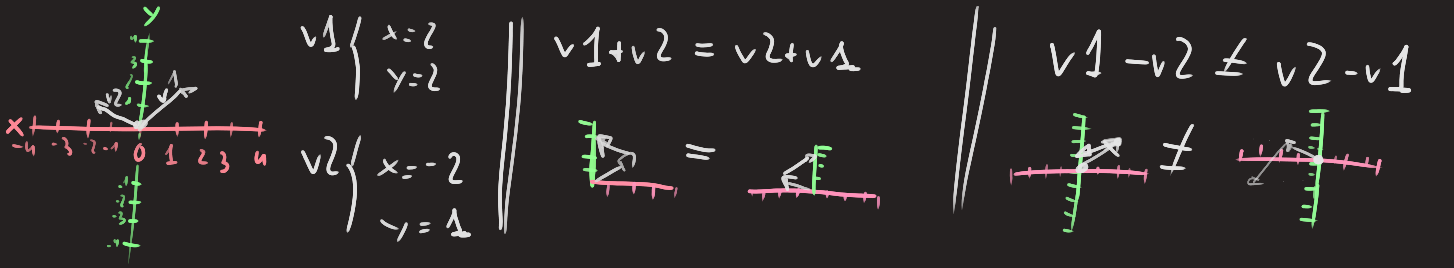
Addition: v1 + v2 = (v1x + v2x, v1y + v2y) - Commutative -> v1 + v2 = v2 + v1
Substraction: v1 - v2 = (v1x - v2x, v1y - v2y) - NON Commutative -> v1 - v2 != v2 - v1
- Why not commutative? -> We are changing the sign of v2 (negate components), then perform an addition of the vectors.
- Ex:
(2,1) - (1,1) = (1, 0)but(1,1) - (2,1) = (-1,0)
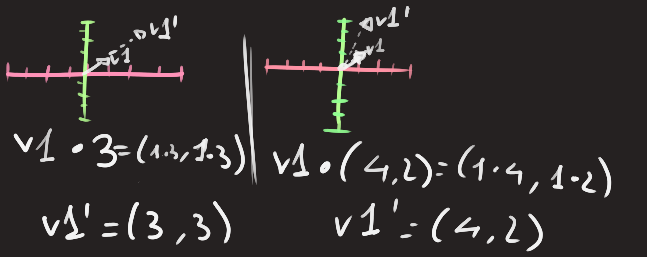
Scalar Multiplication: There are more types, but in the most basic is per component multiplication to scale it. v1 * scalar = (v1.x * scalar, v1.y * scalar) or v1 * v2 = (v1.x * v2.x, v1.y * v2.y).
Vector interpretation depends on its purpose, by themselves vectors don’t define anything but a point. Be clear about what a vector is supposed to be interpreted as (direction, translation, point, worldspace, localspace,…).
sign(vector2D(x,y)): new we will be getting avector2D()in its unit form :v1 / length(v1)
Why are Normalized vectors useful?
When we want to do something along a direction, we don’t want to add further changes than intended. A unit / normalized vector provides just a direction and then we can modify such direction to to fit your magnitude needs.
Length of a vector in 2D (and 3D)
To normalize a vector we need the length of it. In 1D, the main component is already the scalar part of a vector, but in higher dimentions we need other things. We just use basic trigonometry, the Pythagorean Theorem:
vector2D v
v_length = sqrt(v.x ^ 2 + v.y ^ 2)
vector3D u
u_length = sqrt(u.x ^ 2 + u.y ^ 2 + u.z ^ 2)
In higher dimentions, I really don’t know at this point, we’ll figure it out.
Distance between 2 Vectors = length(v2 - v1)
As stated in the beginning, the distance is the length of a vector that joins two points. A vector defines a point, thus a substraction between point2 and point1 will define a vector from point1 to point2. Then we have to get the length of the newly created vector:
vector2D v,u
distance_v_u = length( vector2D( u.x - v.x, u.y - v.y ) )
distance_fun( v , u )
// Same for 3D, but adding z component
Example: Point along a direction
To get a point along a direction represented by an origin point o and an end point v:
- Calculate vector
uthat joins those points - Get the normalized version of
u,u_norm - Multiply
u_normto know where to get a pointu_point - Add
otou_point, to get final pointu_final - Congrats you have got a point between
0oandv
vector2D o,v
vector2D u = v - o
float length_u = sqrt(u.x ^ 2 + u.y ^ 2)
vector2D u_norm = u / length_u
float scalar_value = RandomValue()
vector2D u_point = u_norm * scalar_value
vector2D u_final = u_point + o
Dot Product dot(v1, v2) = v1 * v2 = scalar_value
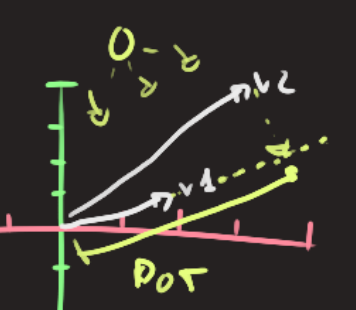
The most starightforward way of understanding a dot product for me is that we are projecting a vector over another. Imagine a light that shines perpendicular to v1, v2 will cast a shadow over v1 that will result in another vector that is a smaller or bigger version of v1.
The result of the operation is a scalar value that indicates the percentage of v1 that is obfuscated by v2. This value can also be negative if the vectors are going in different directions!
vector2D v,u
dot_u_v = v.x * u.x + v.y*u.y
Use Case 1: Squared Unsigned Distance of a Vector
If we run that operation by making sure that u = v, we get the same operation as the length without computing the squared root of it. In some cases, computing the square root is more costly that squaring up the value we want to compare!
Use Case 2: Direction difference between 2 vectors
What makes this operation extremely useful is that when we normalize the vectors and perform the operation, we are returned the cosine of the angle bewteen the vectors!
This ends up helping us by using directly the value as a really fast indication of direction between those vectors.
Further down the line we can obtain the angle between these two vectors in order to get detail information on direction, but taht will come in another post!
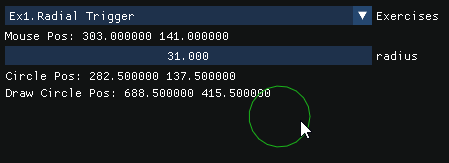
Exercise 1: Radial Trigger
Detect wether a point is inside or outside a circle
Vector2D circle_pos;
float r;
Vector2D mouse_game_space;
float dist = length(mouse_pos - circle_pos);
if(dist <= r)
log("we are in!");
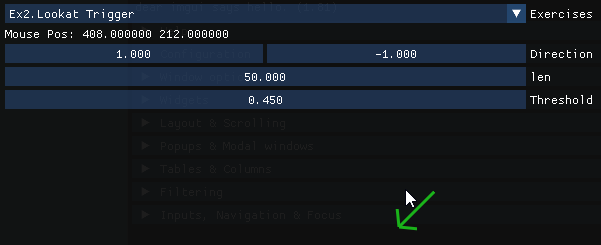
Exercise 2: Look at Trigger
Given a direction and mouse position, know if the direction is looking towards the mouse based on a threshold. Threshold goes form 0 to 1, 1 is super strict (exact direction) and 0 it means perpendicular or closer is looking at mouse.
Vector2D player_pos;
Vector2D player_dir;
Vector2D mouse_game_space;
float threshold;
Vector2D player_mouse_v = mouse_game_space - player_pos;
float dot_value = dot( normalize(player_dir), normalize(player_mouse_v) );
if(dot_value > abs(threshold) && dot_value > 0)
log("we are looking to trigger!");
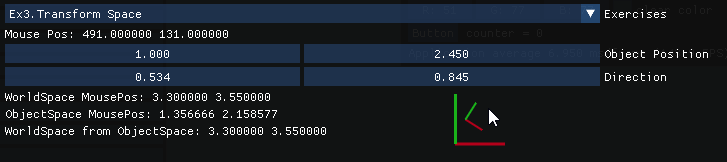
Exercise 3: Transform Space of a Point
Given an arbitrary origin (0,0), an object with a certain position and direction, and a point that is expressed with the object as origin; express the point in origin coordinates (including rotation and translation).
Vector2D object_pos, object_up, object_right; // Obejct values are expressed in world space
Vector2D point_world_space;
// 1 - From world to local space
// Translate to Object Space
Vector2D point_obj_sp = point_world_space + object_pos;
// Move along axis of object
Vector2D point_local;
point_local.x = dot(point_obj_sp, object_right);
point_local.y = dot(point_obj_sp, object_up);
// 2 - From local to world space
// Get from object_space to point space using object axis
Vector2D object_x_axis_point = object_right * point_local.x;
Vector2D object_y_axis_point = object_up * point_local.y;
// These 2 vectors, represent the 2 translations in world space from the worldspace position of the object, to the world position of the point
Vector2D local_point = object_x_axis_point + object_y_axis_point;
// Then to put into full world space, we translate back as if it was from origin
Vector2D world_point = local_point + object_pos;
Afterwords
This series of posts are mainly for my own use. Everyone understands concepts in different ways, after a lot of time battling ways of working (which unfortunately during my studies have been based mostly on crunching) I have found out that having accessible notes on things is the best way. I am awful at remembering thigns correctly and have to check things constantly.
For any other person that does think this theme is useful to them, check Freya Holmer’s Youtube Channel, as most of her content is already uploaded there!
If you want to play with the solutions to the assignments, they can be found on the release page of the website’s repository.